Things to consider when designing, building or curating adaptive content
When developing content for adaptivity, partners should keep several qualities in mind. These include:
Partners should also think about two other factors in particular:
These qualities and factors are described in more detail below.
Granularity refers to the sizes of the pieces of content within the course. There are two granularities that need to be defined: that of individual content items (e.g. a question; an instructional video) and students’ interactions with them, and that of the learning objectives to which each content item aligns.
Granularity of content items and student interactions with them
The granularity of individual content items ties to how Knewton can recommend them to students, and how students’ interactions on them can be communicated back to Knewton and used to inform analytics on the students’ proficiency.
These two granularities are related but distinct. In some cases, these granularities may be the same (e.g., student interactions and recommendations may both be tracked at the item level). In other cases, the granularities will be distinct. For example, student interactions might be communicated to Knewton at a finer granularity (e.g., a student answering the first step of a multi-step assessment correctly) while Knewton recommends content at a coarser granularity (e.g., in the form of an individual assessment item).
Communicating student interactions at the most granular level possible gives Knewton a more precise understanding of a student’s proficiencies, and allows Knewton to provide more targeted and effective Recommendations and Analytics.
Granularity of learning objectives
While the subject matter and pedagogical intent will inform the appropriate granularity for the learning objectives in a course, a useful question to think with in order to arrive at it is “what is the smallest meaningful level at which to track students’ knowledge?”. If the learning objectives are too broad or generic (e.g. Math), remediation for struggling students or learning analytics on student proficiency will not be specific enough to be meaningful. If, on the other hand, the learning objectives are too specific (e.g. individual question level, such as “1+4 = ?”), learning analytics may not be very meaningful. The ideal middle ground for a Math course, for example, depends on the level of the learners: “addition of single-digit integers” might be just right for very early learners, while a broader, all-encompassing “addition” (or even a “review of addition”) learning objective would be more appropriate for students a few more years into their learning. The following examples give some additional sense of reasonable sizes of learning objectives:
It is important for content in an adaptive course to be well-aligned.
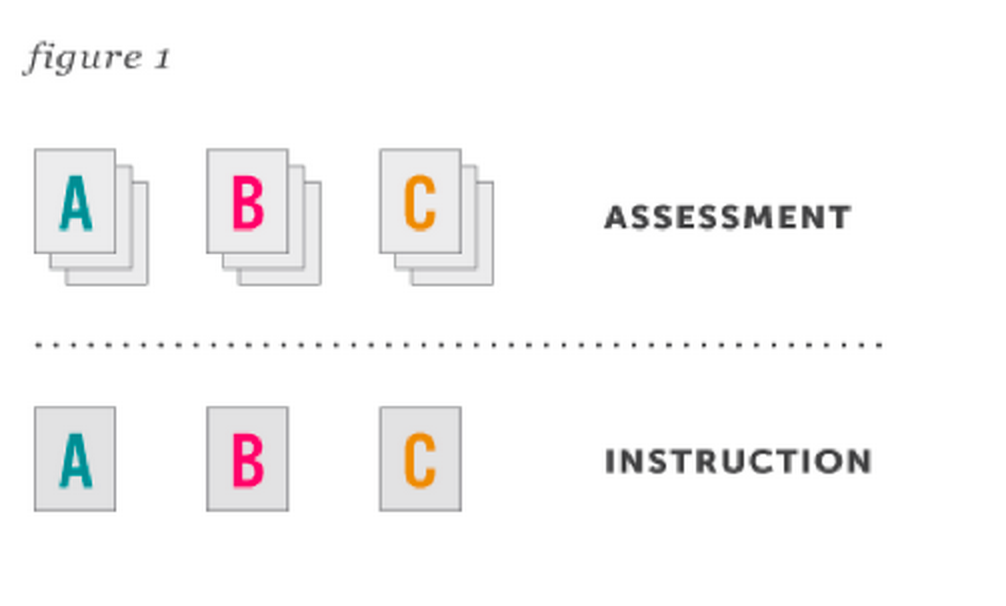
The visual above shows proper content alignment. Here, each letter represents a particular learning objective: A, B, or C. The boxes in the top row represent assessment content assets, each of which assesses a particular learning objective (as labelled). The boxes in the bottom row represent instructional content assets; here, each asset teaches a given objective (as labelled).
Choices about how content is placed in containers can lead to a case of misalignment, as in the diagram below:
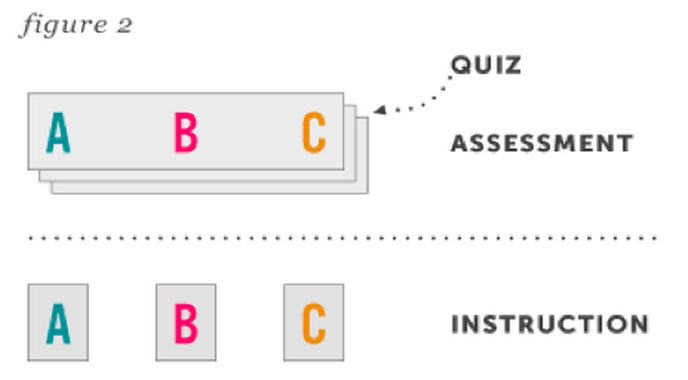
Here, the large box in the top row represents a quiz for which Knewton gets just a single score, but which simultaneously assesses learning objectives A, B, and C. A teacher could not assess a student on the single learning objective A — even if she were already confident in her measure of the student’s proficiencies on learning objectives B and C.
There are other opportunities for inefficiencies to arise. Consider the visual below:
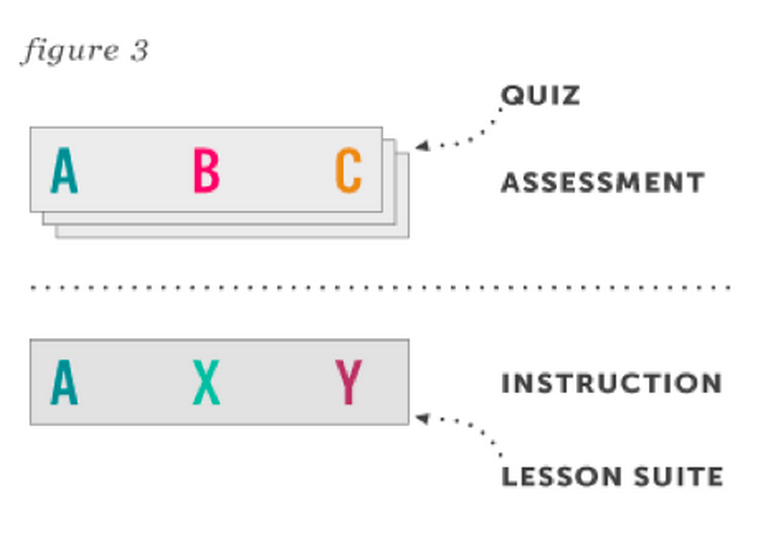
Here, the instructional lessons are contained in a way that does not correspond with the containment of the assessment items. In a scenario like this, after assessing a student on learning objective A and realizing that he does not understand it, an instructor might want to instruct him further on this learning objective. In the above scenario, however, the instructor would need to show the student instructional content about learning objective X and learning objective Y as well. These learning objectives may not be worthwhile for the student to study — perhaps because they are not relevant for the course, perhaps because he is not yet prepared to learn them.
Note: The Knewton system is designed to handle misalignment as best it can. If content has already been developed and grouped in such a way that there is misalignment, our system can still function.
Related to granularity and alignment is the notion of discreteness. A course with discrete content has minimal overlap among both a) learning objectives and b) the content that is aligned to these learning objectives. Discreteness doesn’t mean that learning objectives aren’t related — indeed, in many cases, they build on one another. The important point is that content should be developed or curated around distinct learning objectives, so that instruction and assessment can be more targeted and precise.
Unlike traditional linear courses, which contain units that must be delivered in a certain sequence, modular courses contain units that can be delivered in a variety of orders, depending on the individual’s needs. In general, it is easier to integrate adaptive learning technology into more modular courses.
Because Knewton attempts to find the ideal learning path for each student, there is no predefined order in which a student will encounter recommended content. As a result, the content in a fully adaptive course should contain a minimal amount of “pre-sequencing”; course-level pre-tests, post-tests, and upfront diagnostics, for example, can constrain the degree of personalization within a course, as can strict intra-lesson sequences. A fully adaptive course should also not contain implicit ordering schemes (e.g., lesson numbers or a table of contents) or references within content to moments of instruction that may or may not have happened yet (“As you saw in the last lesson…”).
Modular courses can still contain structure and enable instructors to set strong linear milestones. Knewton Recommendations can be embedded in a way that supports existing product flows, such as instructor-created assignments and comprehensive final exams. Moreover, partners — and the end users of a partner’s product — can help guide Recommendations by setting a goal for each recommendation request and identifying a list of content assets that can be recommended at any time.
Volume of content is the amount of content available for Knewton to recommend. The Knewton system is designed to work with large volumes of content but can also adapt to work with smaller volumes. If a student gets stuck on a certain learning objective and there is little content available to recommend to her, Knewton will recommend the best available piece of content, given that constraint. In other words, “gaps” or “lightness” in content do not block Knewton from functioning.
That said, greater volume of instructional content allows Knewton to present the same learning objective to a struggling student in a variety of ways — content written for different reading levels, for example, or developed in different media — so that students with different learning needs can receive the best possible instruction within the system. The need for differentiated instruction on the same learning objective is greater in “soft” subjects, in which there tends to be less of a prerequisite, or progressive, structure, and thus less to be gained from asking a student to review previous learning objectives.
Similarly, a greater volume of assessment content allows Knewton to make the best recommendations based on student interactions, without fear of showing the same assessment items to a student repeatedly. A lower volume of assessment content may result in Knewton showing the same item to a student on more than one occasion.
A greater volume of content doesn’t mean that every student will interact with that greater volume. Additional instruction or assessment will only be delivered to those students who need it, on a per-learning objective basis.
Assessments have many different components, each of which impacts Knewton’s ability to generate reliable proficiency estimates. The table below gives a sense of the type of data that Knewton makes use of.
Note that these data types are interrelated. For example, the fact that a partner’s assessment items have only three answer choices can be compensated for by the fact that each of the items is instrumented. Note, too, that the preferences expressed below are averages; for example, not every learning objective needs to be highly granular for the system to work, nor does every learning objective need 25 assessment items.
This chart is sorted in terms of decreasing importance to overall product experience.

A partner for which any of the assessment components are merely “viable” should consult with Knewton because that could lead to a degraded adaptive experience for students. Assessments that are not automatically scorable or that rely on rubrics to be scored should also be discussed with Knewton.
For the most part, the above considerations — granularity, alignment, discreteness, modularity, and volume — are important regardless of the way Knewton Recommendations are embedded in a product (e.g., as the primary workflow or a secondary “tutor on the side” supplement). There are, however, times in which the considerations will vary depending on the implementation. Here are two examples:
An algorithmic question is a question where one or more parts can be dynamically or “algorithmically” generated. For example, instead of having separately graphed assessment items for the questions “3 + 5 = ?”, “8 + 2 = ?”, “4 + 7 = ?”, etc., the partner can have a single algorithmic question, which dynamically generates variants of a problem consisting of adding two single-digit numbers. An alternative approach to dynamically generating questions is grouping a number of pre-created variants of a question together into a “pool”, and the question pool, rather than each of its variants, is included in the graph as a single question. Both approaches work the same way with Knewton.
All algorithmic questions should include the metadata field pool_size in the Content Inventory. The value for “pool size” should reflect the number of times the question can be seen before the question would “feel repeated” to a learner. For example, there are 100 possible combinations of adding two single-digit numbers, but if a learner kept seeing the same question template in a row (just with different numbers), it would quickly begin to feel repetitive. Depending on the product and its target user, a reasonable “pool size” for this atom might be 5.